How improving your math skills can help in programming
Paul Orland explores how enhancing one's programming skills can be done through studying up on mathematics and better understanding how the two remain linked.
This article is intended for anyone who wants to improve their math skills, but particularly for programmers who want to apply math to their work. Follow this link and take 35% off Math for Programmers in all formats by entering "ttorland" into the discount code box at checkout.
Fortunately, if you can already write code, you've already trained your analytical thinking skills and mathematical ideas should come naturally. I believe the best way to learn math is with the help of a high-level programming language, and I predict that in the not-so-distant future this will be the norm in math classrooms.
There are several specific ideas that translate directly from programming to math. These will remind you of the skills you already have that you can lean on in your math studies.
Using a formal language
One of the first hard lessons you learn in programming is that you can't write your code like you write simple English. If your spelling or grammar is slightly off when writing an email, the recipient will probably still know what you are talking about. But any syntactic error or misspelled identifier will cause your program to fail. In some languages, even forgetting a semicolon at the end of an otherwise correct statement will prevent the program from running.
One simple example is variable assignment. To a non-programmer, these two lines of Python seem to say the same thing:
x = 5 5 = x
I could read either of these to mean that the symbol x has a value of 5. But that's not exactly what either of these means, and in fact only the first one is correct. The Python statement x = 5 is an instruction to bind the value 5 to the symbol x. On the other hand, you can't bind a symbol to the literal value 5. This may seem pedantic, but you need to know it to write a correct program.
Another example which trips up novice programmers (and experienced ones as well) is reference equality.
>>> class A(): pass ... >>> A() == A() False
If you define a new Python class and create two identical instances of it, they are not equal. You might expect two identical expressions to be equal, but that's evidently not a rule in Python. Because these are different instances of the A class, they are not considered equal.
Be on the lookout for new mathematical objects that look like ones you know but don't behave the same way. For instance, if the letters A and B represent numbers then A x B = B x A. But this is not necessarily the case if A and B are not numbers. If instead A and B are matrices, then the products A x B and B x A are usually different. In fact, it's possible that only one of the products is even possible, or that neither product is possible.
When you're writing code, it's not enough to write statements with correct syntax. The ideas that your statements represent need to make sense to be valid. If you apply the same care when you're writing down mathematical statements, you'll catch your mistakes faster. Even better, if you write your mathematical statements in code, you'll have the computer to help check your work.
Build your own calculator
Calculators are prevalent in math classes because they are useful to check your work. You need to know how to multiply six by seven without using your calculator, but it's good to confirm that your answer of 42 is correct by consulting with your calculator. The calculator also helps you save time once you've mastered concepts. If you're doing trigonometry and you need to know 3.14159 / 6, the calculator is there to handle it so you can think about what the answer means. The more a calculator can do out-of-the-box, the more useful it should theoretically be.

But sometimes our calculators are too complicated for their own good. When I started high school, I was required to get a graphing calculator and I got a TI-84. It had about 40 buttons, each with two to three different modes. I only knew how to use maybe 20 of them, so it was a cumbersome tool to learn how to use. The story was the same in first grade, when even the simplest calculator available had buttons that I didn't understand yet. If I had to invent a first calculator for students, I would make it look something like Figure 1.
This calculator only has two buttons. One of them resets the value to 1 and the other advances to the next number. Something like this would be the right "no-frills" tool for kids learning to count. My example may seem silly, but you can actually buy calculators like this. They are usually mechanical, and sold as "tally counters."

Soon after you master counting, you want to practice writing numbers and adding them. The perfect calculator at that stage of learning might have a few more buttons, like the one in Figure 2.
There's no need for a subtraction, multiplication or division button to get in your way at this phase. As you solve subtraction problems like "5 - 2", you can still check your answer of 3 with this calculator by confirming the sum "3 + 2 = 5." Likewise, you can solve multiplication problems by adding numbers repeatedly. You could upgrade to a calculator that does all the operations of arithmetic when you're done exploring with this one.
In theory, it would be great to add buttons to our calculator as soon as we are ready for them, but that would lead to a lot of hardware floating around. We'd have to solve another problem as well: Our calculators would have to hold more types of data than numbers. In algebra you solve equations with symbols alone, and in trigonometry and calculus you often manipulate functions to create new ones.
Extensible calculators that can hold many types of data seem far-fetched, but that's exactly what you get when you use a high-level programming language. Python comes with arithmetic, a math module and numerous third-party mathematical libraries you can pull in to make your programming environment more powerful, whenever you want. Since Python is Turing complete, you can (in principle) compute anything that can be computed. You only need a powerful enough computer, a clever enough implementation or both.
The best way to learn how Python can help you with math is to dig in and start using it. Working through various implementations yourself can be a great way of cementing your understanding of a new concept, and by the end you've added a new tool to your toolbelt. After trying it yourself, you can always swap in a polished, mainstream library if you like. Either way, the new tools you build or import will lay the groundwork to explore even bigger ideas.
Building abstractions with functions
In programming, the process I describe above is called "abstraction." When you get tired of repeated counting, you create the abstraction of addition. When you get tired of doing so much repeated addition, you create the abstraction of multiplication, and so on.
Of all the ways you can make abstractions in programming, the most important one to carry over to math is the function. A function in Python is a way of repeating some task that may take one or more inputs or produce an output. For example:
def greet(name):
print("Hello %s!" % name)
This lets me issue multiple greetings with short, expressive code:
>>> for name in ["John","Paul","George","Ringo"]: ... greet(name) ... Hello John! Hello Paul! Hello George! Hello Ringo!
This function may be useful, but it's not like a mathematical function. Mathematical functions always take input values and they always return output values, with no side effects. In programming, the functions that behave like mathematical functions are called pure functions. For example, the square function takes a number in and returns the product of the number with itself. When you evaluate the result is 9. That doesn't mean that the number 3 has now changed and become 9. Rather, it means 9 is the corresponding output for the input 3 for the function . You can picture this squaring function as a machine that takes numbers in an input slot and produces result numbers from its output slot.
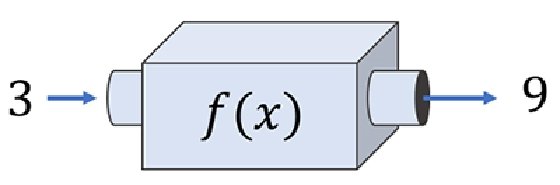
This is a simple and useful mental model. One of the things I like most about it is that you picture a function as an object in and of itself. In math, as in Python, functions are data that you can manipulate independently and even pass to other functions.
Math can be intimidating because some of it is abstract. Remember, as in any well-written software, the abstraction is introduced for a reason: It helps you communicate bigger and more powerful ideas. When you grasp these ideas and translate them into code, you'll open up some exciting possibilities.
About the author
Paul Orland is CEO of Tachyus, a Silicon Valley startup building predictive analytics software to optimize energy production in the oil and gas industry. As founding CTO, he led the engineering team to productize hybrid machine learning and physics models, distributed optimization algorithms and custom web-based data visualizations. He has a B.S. in mathematics from Yale University and a M.S. in physics from the University of Washington.







